《概率论与数理统计》工科类课程教学大纲
《概率论与数理统计》课程教学大纲
课程名称:概率论与数理统计
英文名称:Probability and Mathematical Statistics
课程类型:公共平台课
总学时及学分:48学时 3学分
适应对象:本科二年级(工科类专业)
主要先修课程:高等数学 线性代数
执行日期:2017年9月
一、 课程的性质与任务
性质:概率论与数理统计是研究随机现象客观规律并付诸应用的数学学科,是高等学校工科类本科各专业的一门重要的公共平台课。本课程具有很强的应用性,为后续专业课程提供必要的数学知识和工具。
任务:使学生掌握概率论与数理统计的基本概念,基本理论和基本方法等内容,从而使学生初步掌握处理随机现象的基本思想和方法,具备应用其基本思想和方法解决问题的基本能力。
二、 课程的教学目标
本课程教学的总体目标是:掌握概率论与数理统计的基本概念,以概率论为基础,建立有效的计算方法,进行统计推断;培养学生运用概率论与数理统计方法分析与解决实际问题的能力;培养学生的辩证唯物主义观点、统计观点、逻辑思维能力、分析判断问题能力、创新能力和应用能力,为后续课程的学习及实际应用打下基础。
三、 教学内容及其基本要求
(一)概率论的基本概念
1.随机试验
随机试验的特点
2.样本空间、随机事件
样本空间 随机事件 事件间的关系与事件的运算
3.频率与概率
频率 概率
4.等可能概型(古典概型)
等可能概型的特点 等可能概型中事件概率的计算公式
5.条件概率
条件概率 乘法定理 全概率公式和贝叶斯公式
6.独立性
事件相互独立定义 判定事件相互独立的定理 事件相互独立的结论
教学基本要求:理解样本空间和随机事件的概念;掌握事件间的关系与基本运算;理解事件频率的概念;了解随机现象的统计规律性;掌握概率的计算;理解事件的概念,了解概率的统计定义及公理化定义;理解古典概型的定义;掌握概率的加法公式及它的一些推广;理解条件概率的概念,掌握乘法公式;综合应用加法公式,乘法公式进行概率计算;掌握全概率公式,并掌握什么情况下用该公式;理解事件独立性的概念,了解伯努利概型的定义,掌握判断伯努利概型的方法并用二项公式计算。
教学重点:随机试验的特点;样本空间、随机事件的概念;事件间的关系和事件的运算;频率及概率的概念和性质;古典概型的概念以及古典概型中事件概率的计算公式;条件概率及其性质;乘法定理;全概率公式和贝叶斯公式;事件的独立性及判定条件,判断伯努利概型的方法并用二项公式计算。
教学难点:区分对立事件和互斥事件;用事件间的运算表示一些事件并计算随机事件概率;古典概型中事件发生概率的计算;乘法公式的应用;利用全概率公式和贝叶斯公式求概率;伯努利概型事件中概率的计算。
(二) 随机变量及其分布
1.随机变量
随机变量的定义 随机变量的表示方法
2.离散型随机变量及其分布律
离散型随机变量的定义 两点分布 伯努利实验 二项分布 泊松分布
3.随机变量的分布函数
4.连续型随机变量及其概率密度
概率密度定义 概率密度性质 均匀分布 指数分布 正态分布
5.随机变量的函数的分布
教学基本要求:了解随机变量的概念;理解离散型随机变量及其分布律的概念和性质,连续型随机变量及其密度函数的概念;熟悉几种常见的离散型和连续型分布;会求离散型随机变量的分布律、连续型随机变量的密度函数,并利用它们计算有关事件的概率。理解分布函数的概念,并知道离散型和连续型随机变量的分布函数的性质;掌握离散型和连续型随机变量的分布函数的计算;掌握离散型和连续型随机变量的简单函数的概率问题的求解。
教学重点:随机变量的概念;离散型随机变量及其分布律的概念和性质;三种重要的离散型随机变量的分布:两点分布、二项分布、泊松分布;随机变量的分布函数;连续型随机变量及其密度函数的概念和性质;三种重要的连续型随机变量:均匀分布、指数分布、正态分布;随机变量的简单函数的分布。
教学难点:由连续型随机变量的概率密度函数求分布函数;灵活运用概率分布函数计算各种事件的概率;正态分布的性质、计算和应用;随机变量函数的分布函数。
(三)多维随机变量及其分布
1.二维随机变量
二维随机变量 二维随机变量的分布函数 离散型二维随机变量 连续型二维随机
量
2.边缘分布
边缘分布律 边缘概率密度
3.条件分布
条件概率分布 条件概率性质 条件分布律 条件概率密度
4.相互独立的随机变量
5.两个随机变量的函数的分布
教学基本要求:理解二维随机变量的概念;掌握二维随机变量的边缘分布、联合分布函数等概念;理解二维随机连续型随机变量的联合概率密度的概念及性质;掌握其边缘分布与联合分布的关系,并会计算有关事件的概率;掌握二维随机变量独立性的概念,并会应用独立性来进行计算。
教学重点:二维随机变量及其分布函数的概念;二维离散型随机变量的概念及其联合分布律;二维连续型随机变量的概念及其联合概率密度;边缘分布函数、边缘概率密度;判断随机变量的独立性。
教学难点:由联合概率密度求分布分布函数、边缘概率密度函数;条件概率分布的概念及其求解;两个随机变量的函数的分布。
(四)随机变量的数字特征
1.数学期望
随机变量的数学期望 随机变量函数的数学期望 数学期望的性质
2.方差
方差 方差的性质 切比雪夫不等式
3.协方差及相关系数
协方差 相关系数 协方差的性质
4.矩、协方差矩阵
教学基本要求:理解数学期望的定义,会利用概念求解随机变量的数学期望;掌握离散型及连续型随机变量函数的数学期望的求解方法;熟悉常见分布的数学期望,掌握数学期望的性质,掌握方差的性质及它们之间和数学期望的关系;理解相关性和独立性的关系,会利用它们行进概率的求解;掌握常见分布的方差。
教学重点:数学期望、方差的概念和性质及其计算方法。
教学难点:灵活运用数学期望、方差的概念和性质计算期望和方差,并解决实际问题;协方差及相关系数的定义和性质;矩、协方差矩阵;切比雪夫不等式。
(五)大数定律及中心极限定理
1.大数定律
弱大数定理 伯努利大数定理
2.中心极限定理
独立同分布的中心极限定理 李雅普诺夫定理和棣莫弗—拉普拉斯定理
教学基本要求:了解辛钦大数定理和伯努利大数定理的含义;理解独立同分布的中心极限定理、李雅普诺夫定理和棣莫弗—拉普拉斯定理,并会用相关定理近似计算有关随机事件的概率。
教学重点:大数定理和中心极限定理的基本计算。
教学难点:运用中心极限定理解决实际问题。
(六)样本及其抽样分布
1.随机样本
总体 个体 容量 简单随机样本 样本值
2.直方图和箱线图
直方图 箱线图
3.抽样分布
统计量 常用统计量  分布
分布  分布
分布  分布 正态总体的样本均值与样本方差的分布
分布 正态总体的样本均值与样本方差的分布
教学基本要求:理解总体、个体、样本的概念;理解样本均值、方差和样本矩的概念并会计算;理解统计量的概念;掌握几种常用的抽样分布及其结论;理解分位数的概念;掌握几种重要分布的分位数及查表计算法;了解直方图和箱线图。
教学重点:总体、样本与统计量的概念;样本数据的直方图的绘制;箱线图的作法; 抽样分布的概念;四大抽样分布的计算。
教学难点:统计学的四大分布和抽样分布定理
(七)参数估计
1.点估计
矩估计法 最大似然估计法
2.估计量的评选标准
无偏性 有效性 相合性
3.区间估计
置信区间 置信上限 置信下限 置信水平
4.正态总体均值与方差的区间估计
教学基本要求:理解参数估计的概念,熟练掌握点估计的矩估计法和极大似然估计法;掌握估计量好坏的三个评选标准;了解正态总体均值与方差的区间估计。
教学重点:矩估计和极大似然估计基本原理,评价估计量好坏的标准。
教学难点:运用矩估计和极大似然估计原理解决实际问题。
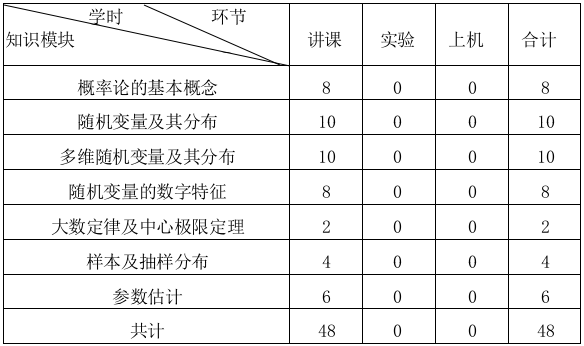
四、 各教学环节学时分配
五、 教学建议
授课过程中,注重重点和难点的透彻讲解,结合习题的练习、分析、讲解,巩固对基础理论的理解,同时根据学情适当调整教学内容,对于偏难的证明内容可以省略,增加计算题的练习。
六、 考核评价方法及要求
本课程以对学生概率论与数理统计基础知识和应用能力的考核为主线,学生最终成绩采用平时成绩、测验成绩和期末成绩相结合的方式。
平时成绩是指任课教师通过记录每个学生上课出勤情况、课堂表现、作业情况等形式给出的成绩,占总评成绩的30%。
测验成绩是指在教学过程中通过对学生进行课堂测验而形成的成绩,测验共分四次,占总评成绩的20%。
期末考试作为一种定量测试手段,这种考试应以评价学生掌握基本知识情况、综合应用概率论与数理统计知识解决实际问题的能力为主,期末成绩占总评成绩的50%。
七、 教材与主要教学参考资源
教材
1.盛骤,谢式千,潘承毅:概率论与数理统计(第四版),高等教育出版社,2009
参考资料
1.龙永红:概率论与数理统计(第三版),高等教育出版社,2001
2.龚德恩:经济数学基础(第三分册:概率统计),四川人民出版社,2005
3.盛骤,谢式千,潘承毅:概率论与数理统计习题全解指南(浙大·第四版),高等教育出版社,2009
4.茆诗松,程依明,濮晓龙:概率论与数理统计教程(第二版),高等教育出版社,2011
5.夏宁茂:新编概率论与数理统计(第二版),华东理工大学出版社,2011
6.同济大学数学系:概率论与数理统计,人民邮电出版社,2017
7.吴赣昌:概率论与数理统计(理工类·第五版),中国人民大学出版社,2017
制定者:王知力 2017年8月
审核者:张 曼 2017年8月
批准者:刘金宪 2017年8月