《线性代数》经管类课程教学大纲
《线性代数》课程教学大纲
课程名称:线性代数
英文名称:Linear Algebra
课程类型:公共平台课
总学时及学分:32学时 2学分
适应对象:本科二年级(经管类专业)
主要先修课程:微积分
执行日期:2017年9月
一、 课程的性质与任务
性质:线性代数是高等学校各专业学生的一门必修的重要基础理论课,它广泛应用于科学技术的各个领域,是后续学习其他课程的基础。本课程以线性方程组解的讨论为核心内容,介绍行列式、矩阵及矩阵的初等变换、线性方程组、向量组的线性相关性、相似矩阵与二次型等内容。本课程既有一定的理论推导,又有大量的复杂运算,有利于培养学生的逻辑思维能力、分析问题和动手解决问题的能力。
任务:通过本课程的学习,要使学生获得线性代数的基本理论和基本运算技能,为相关专业课程的学习提供必需的数学基础知识。通过教学各个环节的实施,逐步培养学生具有一定的抽象概括问题的能力、逻辑推理能力,具有比较熟练的运算能力,综合分析并解决实际问题的能力,严谨处理问题的能力。
二、课程的教学目标
本课程教学的总体目标是:通过本课程教学使学生获得后继课程中经常出现的矩阵、线性方程组等方面的理论知识,熟练掌握矩阵运算、运用初等变换求解线性方程组等基本方法;通过线性代数的概念、内容、思想、方法的讲解,使学生学会由简单到复杂、由具体到抽象,学会分析问题、解决问题的方法。培养学生踏实、认真,求实的做事态度。使学生能用线性代数的理论与方法准确、简明、规范的数学语言表达数学思想的素养。
三、 教学内容及其基本要求
(一)矩阵
1.矩阵的概念
矩阵的概念 几种特殊的方阵
2.矩阵的运算
矩阵的加法 数与矩阵的乘法 矩阵的乘法 矩阵的转置
3.方阵的行列式
二阶行列式 行列式的性质 行列式的计算 拉普拉斯定理
4.矩阵的分块
矩阵分块的概念 分块矩阵的运算
5.可逆矩阵
可逆矩阵的定义 性质
6.矩阵的初等变换
矩阵的初等变换与初等矩阵 求逆矩阵的初等变换法
7.矩阵的秩
矩阵的秩的概念 计算方法
8.矩阵应用的两个例子
矩阵应用的两个例子
教学基本要求:理解矩阵的概念,熟练掌握矩阵的基本运算,熟悉几种特殊的矩阵;理解行列式的概念,掌握行列式的性质,会用降阶法计算行列式,掌握计算n阶行列式的几种常用技巧;理解矩阵分块的概念、分块矩阵的运算;理解可逆矩阵、逆矩阵的概念,了解矩阵可逆的充要条件;理解伴随矩阵的概念,会用伴随矩阵法求逆矩阵;理解矩阵的初等变换以及初等矩阵的概念,了解矩阵的初等变换与初等矩阵之间的关系;掌握求逆矩阵的初等变换法,会用初等变换法解简单的矩阵方程;理解矩阵的秩的概念,会求矩阵的秩。
教学重点:矩阵的概念及运算;行列式的概念及性质;行列式的计算;可逆矩阵的概念;矩阵的初等变换;利用矩阵的初等变换求逆矩阵;矩阵的秩的计算方法。
教学难点:区分矩阵和行列式的区别和联系;行列式的计算方法;逆矩阵的计算方法;矩阵的初等变换和行列式的性质的区别;矩阵秩的概念及计算方法。
(二)线性方程组
1.线性方程组
克拉默法则 线性方程组的消元解法
2.向量及其线性运算
向量的概念 向量的线性运算
3.向量间的线性关系
向量的线性组合 向量组线性相关与线性无关
4.向量组的秩
向量组的极大无关组 向量组的秩与矩阵的秩的关系
5.线性方程组的解的结构
线性方程组的解的结构
教学基本要求:熟练掌握克莱姆法则及线性方程组的消元解法;掌握线性方程组有解的判定定理;掌握n维向量、向量的线性运算及运算法则;理解向量的线性组合,向量组的线性相关与线性无关等概念。掌握判断一个向量组是否线性相关的方法;熟悉有关向量组线性相关性的结论;理解向量组的极大线性无关组、向量组的秩的定义;会求向量组的极大无关组并会用极大无关组线性表示其余向量;理解并掌握齐次线性方程组解的性质、基础解系的定义,会求齐次线性方程组的基础解系,会用基础解系表示齐次线性方程组的全部解;熟悉非齐次线性方程组解的结构,会求非齐次线性方程组的全部解。
教学重点:克拉默法则的应用;线性方程组有解的判定定理;向量的线性相关和无关;向量组的极大无关组。
教学难点:线性方程组的消元解法,线性方程组有解的判定定理;向量的线性组合,向量组的线性相关与线性无关,向量组的极大无关组和秩;线性方程组解的结构。
(三) 矩阵的特征值和特征向量
1.矩阵的特征值和特征向量
矩阵的特征值、特征向量的概念和计算方法 矩阵特征值和特征向量的性质
教学基本要求:理解矩阵的特征值、特征向量的概念和性质,掌握矩阵的特征值和特征向量的求法。
教学重点:矩阵的特征值、特征向量的定义和计算。
教学难点:矩阵特征值和特征向量的计算。
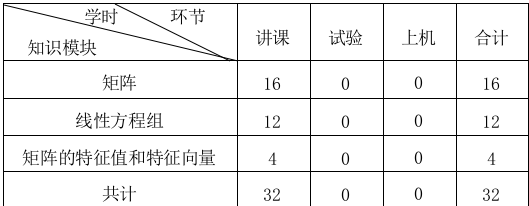
四、 各教学环节学时分配
五、 教学建议
授课过程中,根据学情适当调整教学内容,对于偏难的证明内容可以省略,增加计算题的练习。
六、 考核评价方法及要求
本课程以对学生线性代数基础知识和线性代数应用能力考核为主线,学生最终成绩采用平时成绩、测验成绩和期末考试成绩相结合的方式。
平时成绩是指任课教师通过记录学生上课出勤情况、课堂表现、作业情况等形式给出的成绩,占总评成绩的30%。
测验成绩是指在教学过程中通过对学生进行课堂测验而形成的成绩,测验共分4次,占总评成绩的20%。
期末考试作为一种定量测试手段,这种考试以评价学生综合应用线性代数知识解决实际问题的能力为主,期末成绩占总评成绩的50%。
七、 教材与主要教学参考资源
教材
1.卢刚:线性代数,高等教育出版社, 2009
参考资料
1.同济大学数学教研室:线性代数第四版,高等教育出版社,2003
2.龚德恩:经济数学基础---线性代数第四版,四川人民出版社,2005
3.吴赣昌:线性代数,人民大学出版社,2006
4.郝志峰,谢国瑞,汪国强:线性代数,高等教育出版社,2008
5.同济大学数学系:线性代数第六版,高等教育出版社,2014
6.阎慧臻, 聂宏,王金宝:线性代数,北京理工出版社, 2014
7.张天德:线性代数辅导及习题精解,沈阳出版社,2017
制定者:任焕如 2017年8月
审核者:张 曼 2017年8月
批准者:刘金宪 2017年8月