《微积分一》课程教学大纲
《微积分一》课程教学大纲
课程名称:微积分一
英文名称:Calculus 1
课程类型:公共平台课
总学时及学分:64学时 4学分
适应对象:本科一年级(经管类专业)
主要先修课程:高中数学
执行日期:2017年9月
一、 课程的性质与任务
性质:本课程是高等学校经济类、管理类各专业本科生重要的公共平台课,为后续专业课程,如会计学、管理学、数量经济学、物流管理、财务管理等提供了必要的数学知识与工具。本课程知识在经济活动、管理运作、社会生活等领域中有着广泛的应用。
任务:本课程以微积分基本理论问题为主线,主要向学生讲授微积分学的基本概念、基本理论和基本方法等内容,以及微积分知识在经济管理方面的应用。通过微积分基本理论和方法的学习,培养学生的逻辑推理、量化思维能力,计算能力和创新意识。
二、 课程的教学目标
该课程教学的总体目标是:使学生掌握微积分一这门课程的基本概念、运算及其应用。尤其是微分和积分的思维模式、计算方法需要学生熟练掌握。本课程注重培养学生的逻辑推理能力和量化思维方式,促进素质教育,并为后续专业课程的学习打下良好的基础。
三、 教学内容及其基本要求
(一)函数
1.预备知识
实数与数轴 实数的绝对值及基本性质 区间与邻域
2.函数概念
变量与函数 函数的表示方法 函数定义域
3.函数的几何特征
单调性 有界性 奇偶性 周期性
4.反函数
反函数定义 反函数求法
5.复合函数
复合函数定义 复合函数求法
6.初等函数
基本初等函数 初等函数 隐函数
7.简单函数关系的建立
简单函数关系的建立 经济学中常见的函数关系
教学基本要求:理解函数的概念;掌握函数定义域的求法;会判断函数奇偶性和单调性;了解反函数的概念;会求复合函数;掌握基本初等函数的性质;理解隐函数的概念;会建立简单实际问题中的函数关系式。
教学重点:函数的概念;邻域的概念;函数定义域的求法;函数的单调性,有界性,奇偶性和周期性;反函数的求法;复合函数的求法;基本初等函数的性质;初等函数的概念;隐函数的概念;简单函数关系的建立
教学难点:函数概念的理解;反函数存在条件的理解;隐函数概念的理解
(二) 极限与连续
1.数列极限
数列极限定义 数列极限四则运算法则 夹逼定理
2.函数极限
由函数图形认识函数极限 由函数值认识函数的极限
3.函数极限的性质及运算法则
局部有界性 局部保号性 函数极限运算法则
4.无穷大量与无穷小量
无穷大量与无穷小量 无穷大量与无穷小量阶的比较
5.函数的连续性
函数在一点连续 连续函数 间断点定义及分类
6.闭区间上连续函数的性质
零点存在定理 介值定理 反函数连续性定理
教学基本要求:理解极限的概念;掌握极限四则运算法则;了解两个极限存在准则(夹逼准则和单调有界准则);理解无穷小量、无穷大量的概念;会用等价无穷小求极限;理解函数连续的概念;了解间断点的概念,并会判别间断点的类型;了解闭区间上连续函数的性质。
教学重点:数列极限的概念;函数极限的概念;函数极限的四则运算法则;无穷大量和无穷小量的概念;利用等价无穷小求极限;函数连续的概念;间断点的概念,间断点的类型;了解初等函数的连续性闭区间上连续函数的性质。
教学难点:极限概念的理解;两个极限存在准则(夹逼准则和单调有界准则)的理解;利用等价无穷小求极限;间断点的概念的理解。
(三) 导数与微分
1.导数概念
导数的定义 函数在可导点的局部性质
2.导数运算与导数公式
导数的四则运算 反函数的导数 导数基本公式
3.复合函数求导法则
链式法则 取对数求导法 隐函数求导法则
4.微分及其计算
微分定义 微分运算法则 复合函数的微分 一阶微分形式不变性
5.高阶导数与高阶微分
高阶导数 高阶微分
6.导数与微分在经济学中的简单应用
边际分析 弹性
教学基本要求:理解导数和微分的概念;理解导数的几何意义;掌握函数的可导性与连续性之间的关系;掌握导数的四则运算法则和复合函数的求导法;了解反函数求导法则;掌握基本初等函数的导数公式;了解微分的四则运算法则和一阶微分形式不变性;了解高阶导数的概念;掌握函数二阶导数的求法;会求隐函数和参数方程所确定的函数的导数;会求边际函数。
教学重点:导数和微分的概念;导数的几何意义;函数的可导性与连续性之间的关系;导数的四则运算法则;复合函数的求导法则;反函数求导法则;两个重要极限;基本初等函数的导数公式;函数高阶导数的求法;隐函数求导法则;参数方程所确定的函数的求导法则;边际函数的理解。
教学难点:导数和微分概念的理解;复合函数求导法则的掌握;反函数求导法则的掌握;一阶微分形式不变性的理解。
(四) 中值定理与导数的应用
1.微分中值定理
费马定理 罗尔中值定理 拉格朗日中值定理 柯西中值定理
2.泰勒公式
泰勒定理 麦克劳林公式
3.洛必达法则
未定式 洛必达法则
4.函数的单调性与凹凸性
一阶导数的符号与函数的单调性 二阶导数符号与函数的凹凸性
5.函数的极值与最大(小)值
极值 最大值和最小值
6.函数作图
渐近线 函数作图步骤
教学基本要求:理解罗尔定理和拉格朗日定理;了解柯西定理;了解泰勒公式;掌握洛必达法则;理解函数的极值概念;掌握用导数判断函数的单调性和求极值方法;会用导数判断函数图形的凹凸性;会求拐点;会描绘函数的图形(包括水平和铅直渐近线);会求解较简单的最大值和最小值的应用问题。
教学重点:函数的极值概念;费马定理;罗尔中值定理;拉格朗日中值定理;洛必达法则;利用导数判断函数的单调性和凹凸性;利用导数求极值;驻点、拐点和极值点的理解;求解较简单的最大值和最小值的应用问题。
教学难点:拉格朗日中值定理的理解;驻点、拐点和极值点的理解;利用导数解决最大值和最小值的应用问题。
(五) 不定积分
1.原函数与不定积分的概念
原函数 不定积分
2.基本积分公式
基本积分公式表 利用积分公式求积分
3.凑微分法和分部积分法
凑微分法 分部积分法
4.换元积分法
幂函数代换 三角代换
教学基本要求:理解原函数的概念;理解不定积分的概念与性质;掌握基本初等函数的积分公式;掌握不定积分的换元法与分部积分法。
教学重点:原函数的概念;不定积分的概念与性质;基本初等函数的积分公式;不定积分的直接积分法、换元积分法和分部积分法。
教学难点:不定积分的换元法与分部积分法的理解。
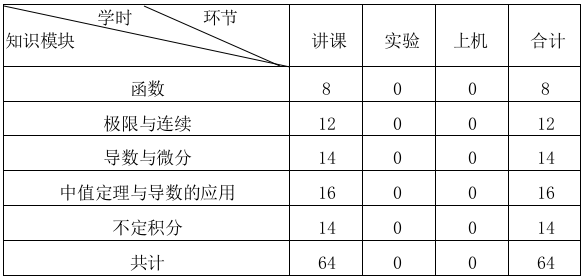
四、 各教学环节学时分配
五、 教学建议
授课过程中,根据学情适当调整教学内容,对于偏难的证明内容可以省略,增加计算题的练习。
六、 考核评价方法及要求
本课程以对学生微积分基础知识和应用能力的考核为主线,学生最终成绩采用平时成绩、测验成绩和期末考试成绩相结合的方式。
平时成绩是指任课教师通过记录每个学生上课出勤情况、课堂表现、作业情况等形式给出的成绩,占总评成绩的30%。
测验成绩是指在教学过程中通过对学生进行课堂测验而形成的成绩,测验共分4次,占总评成绩的20%。
期末考试作为一种定量测试手段,这种考试以评价学生综合应用微积分知识解决实际问题的能力为主,期末考试成绩占总评成绩的50%。
七、 教材与主要教学参考资源
教材
1.朱来义:微积分第三版,北京:高等教育出版社, 2009
参考资料
1.朱来义:微积分中典型例题分析与习题,第二版,北京: 高等教育出版社, 2009
2.李红英:微积分同步辅导与习题全解,华东理工大学出版社,2015
3.王龙:微积分基础,华东理工大学出版社,2015
4.赵树嫄:经济应用数学基础(一)微积分,第四版,中国水利水电出版社,2016
6.邹彪:经济数学——微积分,西安电子科技大学出版社,2016
7.高源:经济数学——微积分同步辅导及习题讲解,第三版,水利水电出版社,2017
制定者:崔 玮 2017年8月
审核者:张 曼 2017年8月
批准者:刘金宪 2017年8月